Asset Allocation using Stochastic Dominance

Stochastic Dominance has been applied in the domain of finance for several decades. It is most commonly applied in investment namely portfolio diversification, defining risk, estimating bankruptcy risk, capital structure, and determining option’s price bounds. In this blog, we discuss the application of Stochastic Dominance in portfolio selection.

• Portfolio selection or asset allocation is one of the few general problems in the investment industry. Financial professionals have been developing various models to solve this problem. We start by defining an asset universe, that is, a set of assets which are considered to construct a portfolio. In portfolio construction models, we then make a choice of a subset the assets (in the asset universe) and create a portfolio. Basically, there are three main types of such models: mean-risk models (e.g., Markowitz model), expected utility maximization, and Stochastic Dominance models.
• Stochastic Dominance has been considered by experts in econometrics and quant analysts as the best model for asset allocation. In particular, second order stochastic dominance (SSD) is the most desirable model as it captures behavior of a risk-averse investor. Mean-risk models are convenient from a computational point of view, but in many cases, depending on the risk measure that is used, they may lack a rational, theoretical basis for making a choice. Thus, the validity of the results provided is often questionable. Expected utility maximization is usually difficult to put into practice since the choice of a suitable utility function is somewhat subjective. Stochastic Dominance has a sounder theoretical basis for making choice under risk. Second order Stochastic Dominance (SSD) is particularly important in investment problems since it describes the preference of rational and risk-averse decision-makers. To get a clearer understanding, let’s go through a simple explanation of what stochastic dominance is.

Stochastic Dominance gives us a sense of a partial order between random variables. The concept arises in decision theory and decision analysis in situation where one gamble (a probability distribution over possible outcomes, also known as prospects) can be ranked as superior to another gamble for a broad class of decision-makers. For example, in finance, when comparing the relative value of two investments (asset A and asset B) the one whose probable rate of return exceeds the other, at any level, is stochastically dominant.
There are two common types of Stochastic Dominance that are applied in finance: First order Stochastic Dominance (FSD) and Second order Stochastic Dominance (SSD). In general, these terms are used for two purposes. Suppose two investment portfolios have outcomes distribute as two corresponding distributions F(x) and G(x). First order Stochastic Dominance is used when we want to know which portfolio will yield a higher outcome if we compare two distributions F(x) and G(x). But in practice, FSD conditions may not be possible to satisfy for a given set of return data. In contrast, for the same return dataset, Second order Stochastic Dominance (SSD) can be easier to satisfy. The benefit of SSD, set against other approaches, is that a portfolio constructed in this way is less risky if the average returns are the same across both distributions F(x) and G(x). In Second order Stochastic Dominance, when a portfolio is less risky than the other, we say that portfolio is non-dominated with respect to Second order Stochastic Dominance, and the riskier portfolio is said to be dominated with respect to Second order Stochastic Dominance.

Stochastic Dominance models are known to be demanding from a computational point of view. Many financial practitioners have found applying stochastic dominance in portfolio selection impractical. Stochastic dominance relations, and SSD in particular, are the soundest theoretical basis for making rational choices, corresponding to observed economic behavior. Unfortunately, they are difficult to apply in practice.
With a vision of being one of the leaders in the innovation of optimization, risk modelling and financial analytics, OptiRisk has worked on Stochastic Dominance since early 2000s. We have carried out extensive research on Stochastic Dominance modelling and found solution for the computational problem. Our models support decision-makers in making meaningful decisions, according to observed economic behavior, and at the same time preserve computational tractability. We have also expanded the application of SSD in model and index enhancement and incorporate it with sentiment analysis.
Some technical papers on stochastic dominance analysis produced by OptiRisk are listed below:

• Portfolio Construction based on Stochastic Dominance and Target Return Distributions
• Processing Second-Order Stochastic Dominance Models Using Cutting Plane Representations
• An Enhanced Model for Portfolio Choice with SSD Criteria: A Constructive Approach
• Enhanced Indexation Based on Second-Order Stochastic Dominance
• Using Market Sentiment to Enhance Second Order Stochastic Dominance Trading Models

You can find full versions of these papers totally free here.

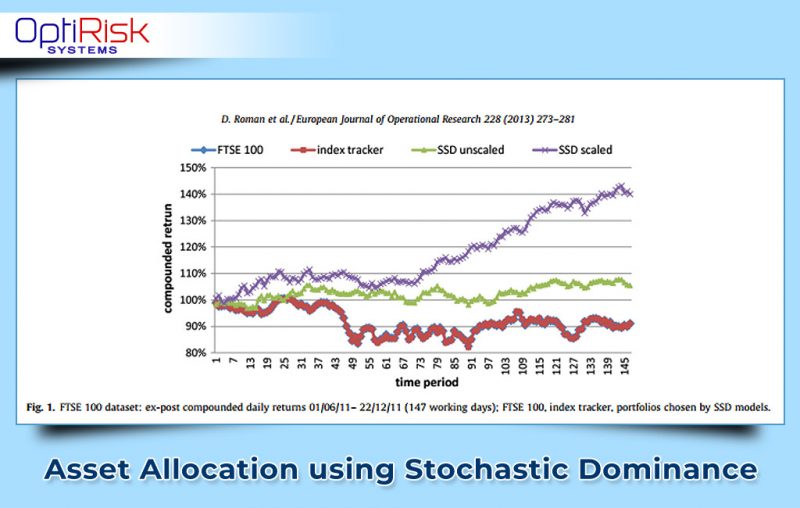
These papers have made significant contribution to the domain of Stochastic Dominance, including solution and scaling up. In these papers, we consider the problem of constructing a portfolio which is non-dominated with respect to Second order Stochastic Dominance (which means this portfolio is less risky) and whose return distribution has specified desirable properties. Therefore, an optimal portfolio is chosen. Different approaches are implemented to solve the computational constraint in different papers. We present the computational study in great details, which demonstrate the effectiveness and scale-up properties of the solution algorithm as applied to the SSD model. The SSD model is also further researched and shows impressive results when being applied in enhancing model for portfolio choice, enhancing indexation in active portfolio management, and coupling with sentiment analysis in optimization model.

Sentiment analysis is another domain where OptiRisk has undertaken extensive research and publication. Please visit our website to take a look at these papers and publication.
As a result of the research contributions made by OptiRisk in (i) the modeling and (ii) computational solution of these SSD models, a quant fund manager can apply SSD to construct practical portfolios.
To learn more about our research of (i) Stochastic Dominance modeling and (ii) computational (software) realizations please look out for our follow-up blog here.
Please feel free to get in touch at info@optirisk-systems.com for any further details.