FortSP is a solver for stochastic programming (SP) problems in which the underlying optimization model is a linear programming problem. It is used as the solver for the SPInE modelling system; FortSP may be used on its own to solve problems presented in SMPS format.
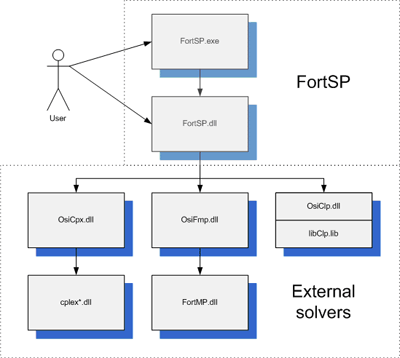
FortSP is available as a standalone program and as a library with interface in the C programming language. It has a powerful plugin system for connecting external solvers through the COIN-OR Open Solver Interface (OSI). These embedded solvers are used to optimize the deterministic equivalent problem and also the sub-problems in the decomposition methods. Currently supported solvers include CLP, CPLEX and FortMP, other OSI-compatible solvers can be easily connected.
FortSP is designed to solve both two-stage and multi-stage recourse problems. The objective of an SP problem is to find the best values for first-stage decision variables to be chosen now, given distributions for alternative scenarios (data paths) spanning future time stages. Each uncertain value in the model data is described by a finite sampling of discrete values. In each future stage there are decision variables to correspond with each possibility (known as ‘recourse actions’), and these are constrained by linear forms connecting that stage to previous stages. See “Introduction to Stochastic Programming” by J.R. Birge and F. Louveaux for detailed problem statement and mathematical background.
Algorithm in FortSP :
The following decomposition algorithms are available in FortSP for solving this class of problems referred to as ‘Here-and-Now’ (HN) problems:
- Benders’ decomposition – L-shaped method
- Variant of level decomposition
- Nested Benders’ decomposition
The first two methods are applicable for two-stage problems and the last allows to solve multi-stage problems. These algorithms take advantage of a specific structure of stochastic programming problems and make it possible to solve problems with large number of scenarios.
Alternative solution approach is to formulate a deterministic equivalent of an SP problem and use an LP solver to optimize it. FortSP fully supports automatic formulation of deterministic equivalent problems either with implicit or explicit nonanticipativity constraints. This method is feasible and sometimes advantageous especially if the number of scenarios is relatively small.
FortSP can also formulate deterministic equivalents of two-stage problems with chance constraints and integrated chance constraints. For integrated chance constraints an efficient cutting-plane algorithm is provided.
In addition to finding HN ‘Here-and-Now’ values for decision variables in the first time-stage the system may extend this to recourse values for the various scenarios in future time-stages, and may also evaluate the following special models:
- WS ‘Wait and See’:- This is a family of models, one for each scenario, and the weighted average of solutions for each scenario (solved by assuming that all data were already known) gives the expected WS solution.
- EV ‘Expected Value’: – The solution based on assuming all data will take its expected value
The following stochastic measures may be derived from outputs of the three models:
- EVPI ‘Expected Value of Perfect Information’
- VSS ‘Value of Stochastic Solution’
